Sumace pro začátečníky
Tento článek píši pro studenty, kteří narazí na sumace a při pohledu na divný zápis se zděsí a chtějí to vzdát. Dejte matematice ještě šanci, není to tak těžké, jak to vypadá.
Inspirací pro tento článek byl tento výraz:
`sum_(k=4)^13 20-3k`
Co znamená následující příklad?
`sum_(k=1)^3 k`
Je to součet čísel od jedné do tří. V každém opakování dosadíme za k aktuální hodnotu a pak číslo zvětšíme o jedničku a pokračujeme, dokud k nemá hodnotu 3. Matematicky vyjádřeno:
`sum_(k=1)^3 k=1+2+3=6`
Suma často pracuje s výrazy. Asi nejjednodušší formou je vložit neznámou x jako výraz.
`sum_(i=2)^3 x`
Tentokráte budeme sčítat neznámou x tolikrát, kolik je rozdíl mezi číslem nad a pod znakem sumace:
`sum_(i=2)^3 x=x+x=2x`
Rozepsat si sumaci na součty je samozřejmě možné, ale při větším počtu opakovaní poněkud nepraktické. Naštěstí máme k dispozici vzorečky. Začněme opět u součtu posloupnosti hodnot. Když se podíváte na výraz 1+2+3, tak se dá vyjádřit také jako 3*2. Trojka je počet opakování a dvojka je prostřední číslo řady. Není to náhoda. Vzoreček má následující formální vyjádření:
`sum_(i=m)^n i=((n-m+1)(m+n))/2`
Pojďme si to vyzkoušet:
`sum_(i=1)^4 i=((4-1+1)(1+4))/2=(4 xx 5)/2=20/2=10`
`sum_(i=1)^4 i=1+2+3+4=10`
Vzoreček pro výpočet součtu opakování výrazů:
`sum_(i=m)^n x=(n-m+1)x`
A opět si to zkusíme v praxi:
`sum_(i=3)^6 x=(6-3+1)x=4x`
`sum_(i=3)^6 x=x+x+x+x=4x`
Pojďme dále. Například že sčítání či odečítání lze vytáhnout ven ze sumace, což se nám bude hodit k vyřešení prvního příkladu. Nejdříve si ukážeme pravidlo:
`sum_(k=1)^3 1+k=sum_(k=1)^3 1+sum_(k=1)^3 k`
Jak dále? Aplikujeme jednoduchá pravidla, které jsem ukázal výše:
`sum_(k=1)^3 1=(3-1+1)1=3`
`sum_(k=1)^3 k=((3-1+1)(1+3))/2=(3 xx 4)/2 = 6`
Výsledek je tedy 9. To si snadno ověříme rozepsáním:
`sum_(k=1)^3 1+k=(1+1)+(1+2)+(1+3)=2+3+4=9`
Teď už nám chybí poslední pravidlo, které nám zjednoduší zápis hledané formule. Také násobení můžeme přesunout před sumaci:
`sum_(i=m)^n 3x=3sum_(i=m)^n x`
A ukázka:
`sum_(i=1)^3 3x=3x+3x+3x=9x`
`3 sum_(i=1)^3 x=3(x+x+x)=3 xx 3 x = 9x`
Nyní můžeme přejít k řešení úlohy. Stačí jen aplikovat pravidla, která jsem vysvětlil výše:
`sum_(k=4)^13 20-3k=sum_(k=4)^13 20-3sum_(k=4)^13 k=(13-4+1)20-3*((13-4+1)(13+4))/2=`
`=10*20-(3*(10*17))/2=200-(3*170)/2=200-255=-55`
Pro kontrolu jsem napsal jednoduchý prográmek v Javascriptu. Zvolte tlačítko Run a vyjede vám výsledek. Pokud si chcete kód upravit pro svou rovnici, zvolte tlačítko Fork. Další užitečné vzorečky najdete na wikipedii sumace.
Pokud chcete mít na svém wordpress blogu také matematické výrazy, doporučuji si nainstalovat jednoduchý plugin pro Mathjax. A pak můžete jednoduše psát v AsciiMath notaci.

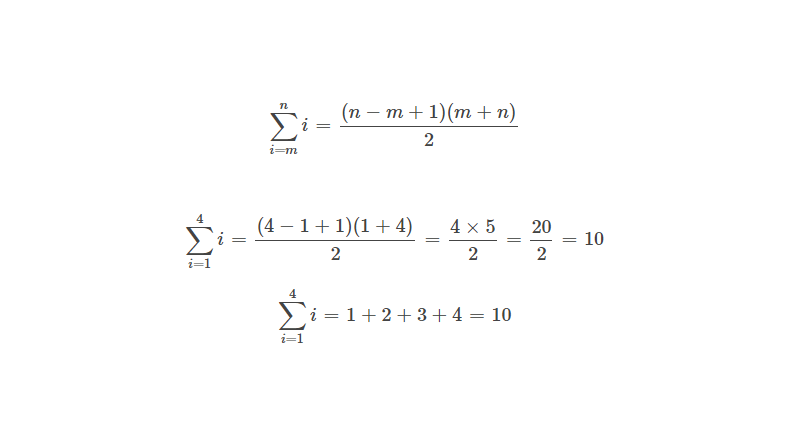

Úžasné, děkuji za skvělý článek. Nyní projdu do druhého semestru.